图像分割基本方法

输入输出

下面讲解一下模型的输入与输出的形式。尤其是输出。

输入 (Input)：RGB图像 (height, width, 3) 或者灰度图 (height, width, 1) 。第三个维度是通道数，RGB图像有三个通道，而灰度图只有一个通道。在第一维再加一个batch size 就是 RGB 图像 (batch_size, height, width, 3) / 灰度图 (batch_size, height, width, 1)

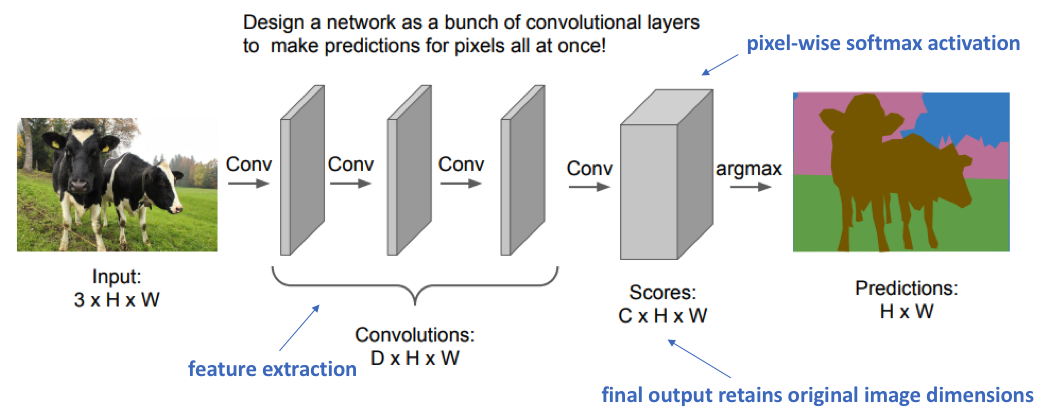
输出 (Output) ：和处理分类任务的时候类似，通过为每个可能的类别创建一个输出通道，并one-hot来编码类别标签，来表示target。如下图所示。

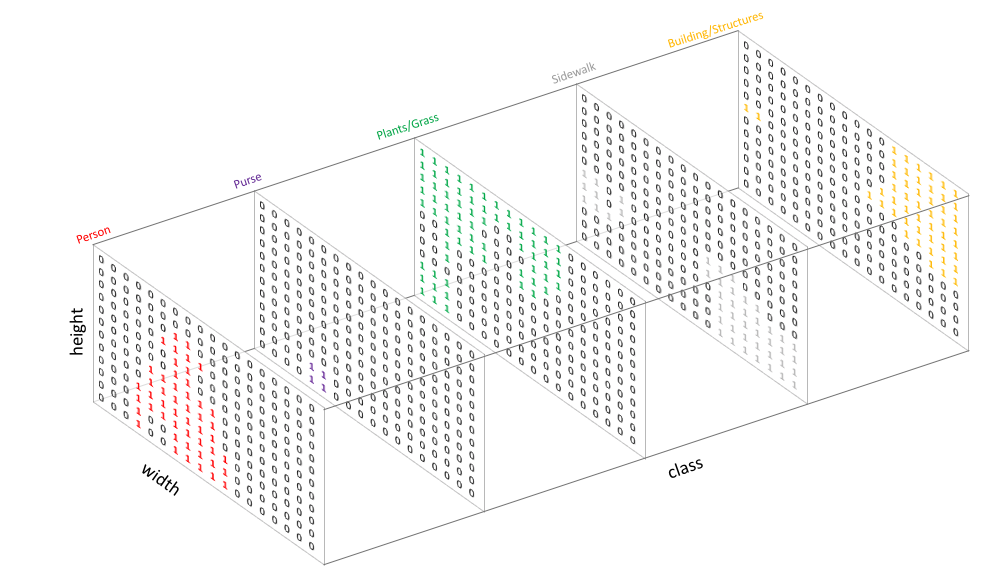
Source An overview of semantic image segmentation.

通过采用每个深度方向像素向量的 $argmax$，可以将预测折叠到一张分割图中（如下图所示）

注意：对于视觉清晰度，这里标记了一个低分辨率预测图。 实际上，分段标签分辨率应匹配原始输入的分辨率。

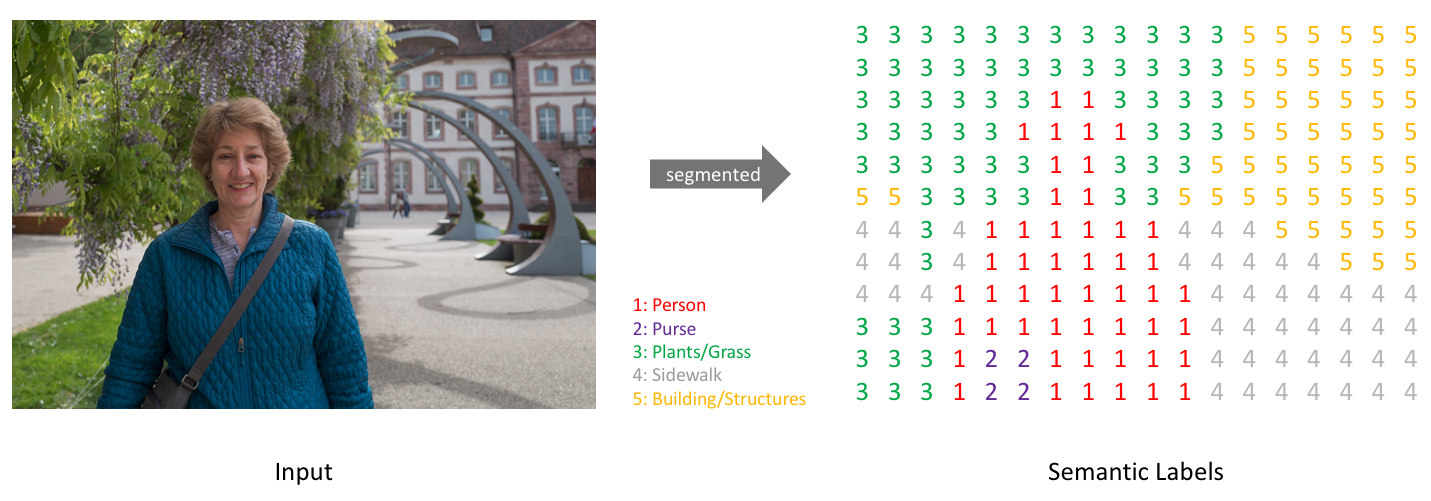
Source An overview of semantic image segmentation.

可以很容易地检查一个目标，把它覆盖到观察。

Source An overview of semantic image segmentation.

当覆盖target（或预测）的单个通道时，将此称为 mask，该 mask 照亮存在特定类的图像的区域。

当不做 $argmax$ 直接输出target的时候，输出的形状应该是 (batch_size, num_class, height, width)，每张图片的每个通道的里是非0即1的one-hot向量 。

而当对target进行 $argmax$ 后，输出的形状应该是跟输入同一形状 (batch_size, height, width)。

模型结构

这一节将简要地介绍用于图像分割的最经典的深度学习模型结构：编码器/解码器结构 (Encoder/Decoder structure)

全连接到1×1卷积

回想一下在分类任务当中的CNN网络都是几个卷积层和池化层组成，最后是几个全连接层。然而一张图片经全连接层之后的输出是个一维的向量。这对分类任务中，只需要知道图片的内容，而不关心其位置十分适用。如果想得到上面的二维的输出，那么就不能采用全连接层。在2014年发表的 Fully Convolutional Network 的论文认为，最终的全连接层可以被认为是做一个覆盖整个区域的1x1卷积。即如下图所示。

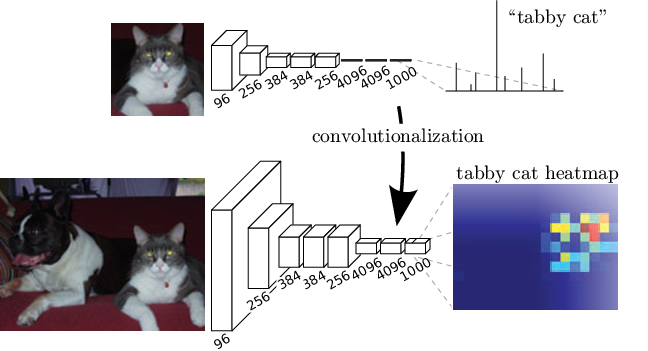
Source Fully Convolutional Networks for Semantic Segmentation

这里使用1×1的卷积替代全连接层还有一个好处：那就是输入的图片形状不在固定了。由于全连接层的输入必须固定形状的，所以输入模型的图片一般都要先resize到固定的shape，而使用1×1卷积代替全连接层之后变不在存在这一问题。在推理的时候，不需要再对图片进行resize，从而最好可能会导致输出的图片的失真。

这么一个不断加深网络并不断增加通道数来提取浅层信息和深层特征的过程就是编码器 (Encoder)。

上采样

很明显上方编码器的输出与想要的输出还是存在一定的差距。想要的是一个与原输入同尺寸的输出。如果直接用双线性插值来进行上采样，将encoder的输出直接resize到原图的大小，这可能会有一定的效果，但一定不是最理想的。

那么还有一张方法，每层我们设置一定数量的padding，只是用卷积层，取消所有池化层。这样堆叠多个卷积层最后得到的输出变能够跟原图保持同尺寸，输出对应像素点的类别了。就如下图所示一样。

Source CS231n: Deep Learning for Computer Vision(2017) Lecture 11

然而，要想抽取出深层的特征，那么这个网络就需要足够的深，通道数足够多。而由于所有的层都保留了原尺寸，所以他的计算量是极其巨大的。所以这种方法也没有被广泛使用。

最终还是采用了先通过编码器将图像的特征映射到高维空间，这之后再通过解码器上采样，将特征恢复到图片的原尺寸。上采样的这一部分网络叫做解码器 (Decoder) 。

而上采样主要采用的是一种可以学习参数的转置卷积 (Transposed Convolution) /反卷积 (Deconvolution) 的非线性上采样。

所以整个模型结构可以理解为是一个先下采样再上采样的过程，如下图所示。

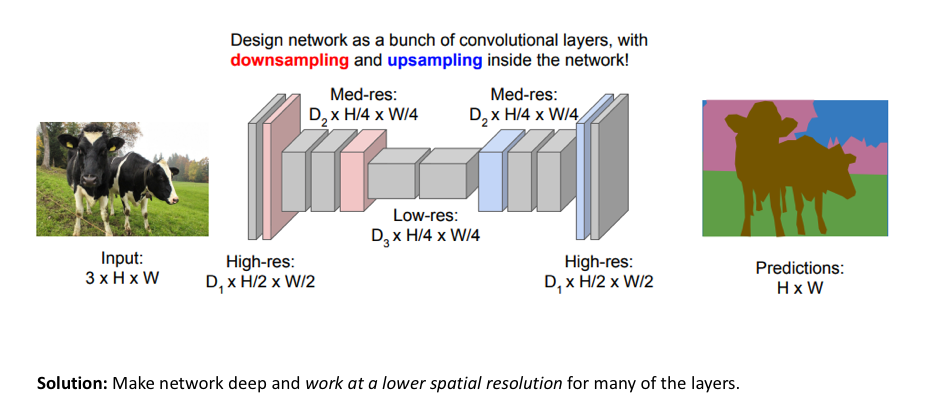
Source CS231n: Deep Learning for Computer Vision(2017) Lecture 11

几种上采样 (upsample)方法

上采样的几种方法的名字很容易混淆，下面将一一捋清。

上采样 (upsample) 主要有三种方法：转置卷积 (Transpose Convolution)、上采样 (unsampling) 和 反池化 (unpooling)。讲到这里有两个地方需要提前解释清楚。

1. 上采样 (upsample) 是这些方法的总称，而上采样 (unsampling) 是一种具体的方法。主要一个是 ”up”，一个是 ”un”，所以这样要将英文给写出来。
2. 这里的的转置卷积 (Transpose Convolution) 还有很多名称：反卷积 (Deconvolution)、逆卷积 (Inverse Convolution)、Upconvolution、Fractionally strided convolution、Backward strided convolution。最常用的是转置卷积和反卷积这两个名称。这里主要使用转置卷积这个名称。

这一节将简单介绍三种方法的区别，然后主要讲解转置卷积的原理，和输出形状的计算公式。

三种方法对比

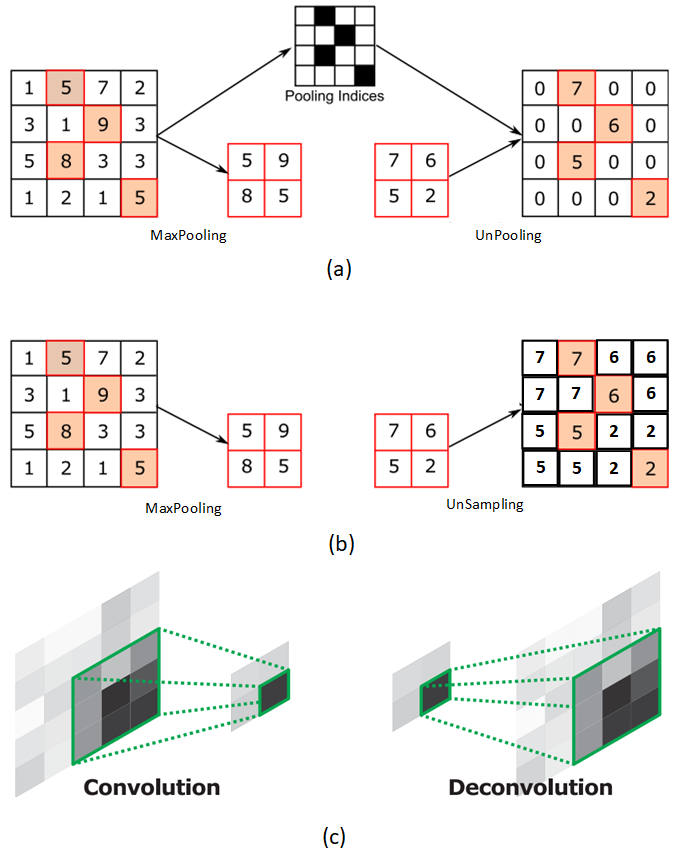
Source 真的没找到 图 (c) 似乎来源于 Learning Deconvolution Network for Semantic Segmentation

图 (a) 是反池化。在MaxPooling的时候会保留Pooling使用的最大值的索引，然后UnPooling的时候使用索引将输入映射到feature map中，而其他位置全填0。

再对比图 (b)，反池化和上采样很明显的差别就是没有Pooling Indices这个输入，而是直接将输入特征扩充到feature map中

图 (c) 是转置卷积，通过有参数的卷积核将输入特征映射到feature上，重复的地方会进行叠加。

转置卷积原理

在这之前要先引入卷积矩阵 (Convolution Matrix) 这一概念。

卷积矩阵

首先让我们来回顾一下卷积的操作过程。

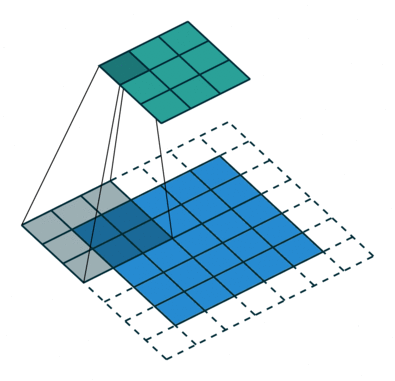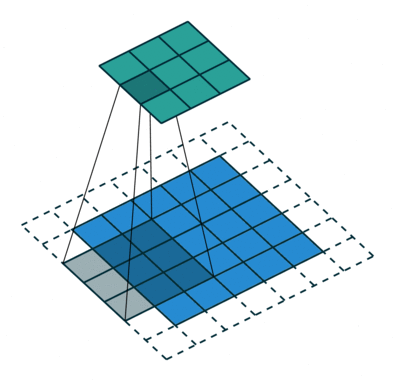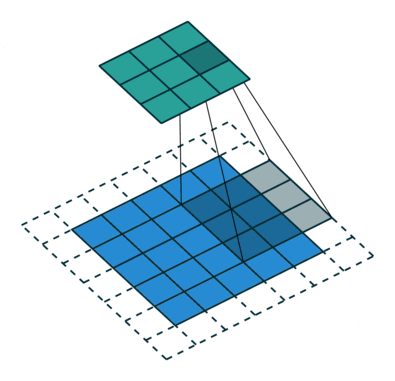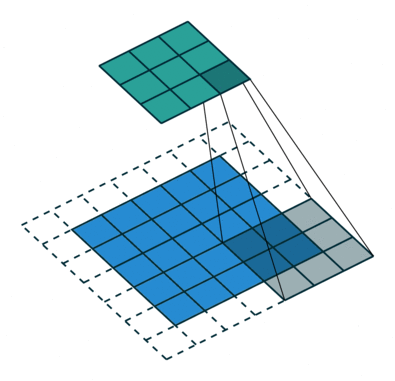
给定输入$i= \begin{bmatrix} x_{11} & x_{12} & x_{13} & x_{14} \newline x_{21} & x_{22} & x_{23} & x_{24} \newline x_{31} & x_{32} & x_{13} & x_{34} \newline x_{41} & x_{42} & x_{43} & x_{44} \newline \end{bmatrix}$，卷积核$K= \begin{bmatrix} w_{11} & w_{12} & w_{13} \newline w_{21} & w_{22} & w_{23} \newline w_{31} & w_{32} & w_{13} \newline w_{41} & w_{42} & w_{43} \newline \end{bmatrix}$。大家可以计算一下卷积操作之后的输出是什么。

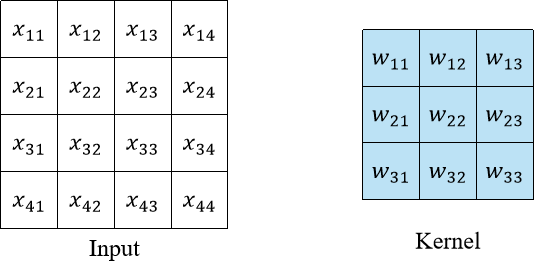
Source XuHao

大致是按下图方式进行计算。

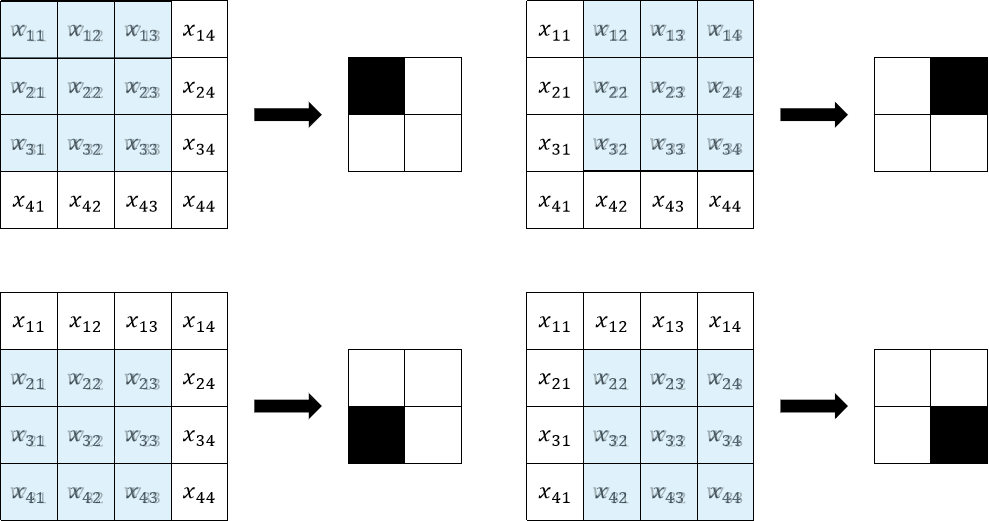
Source XuHao

下图是一个动画演示，3×3 的卷积核在 4×4 的蓝色输入上进行没有 padding 和单位 stride 的卷积操作，得到 2×2 的灰色输出

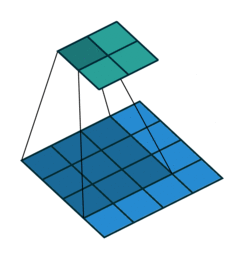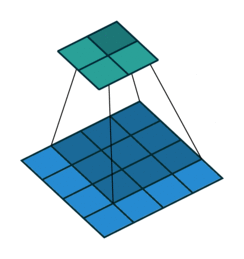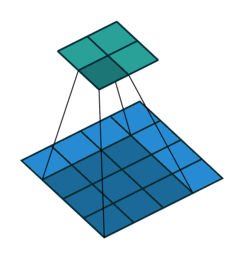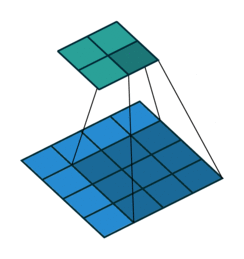
Source Convolution arithmetic

最后的卷积计算结果应该是

$$ \begin{bmatrix} w_{11}x_{11}+w_{12}x_{12}+w_{13}x_{13} \hphantom{00000} & w_{11}x_{12}+w_{12}x_{13}+w_{13}x_{14} \newline +w_{21}x_{21}+w_{22}x_{22}+w_{23}x_{23}\hphantom{00000} & +w_{21}x_{22}+w_{22}x_{23}+w_{23}x_{24} \newline +w_{31}x_{31}+w_{32}x_{32}+w_{33}x_{33}, \hphantom{00000} & +w_{31}x_{32}+w_{32}x_{33}+w_{33}x_{34} \newline \newline w_{11}x_{21}+w_{12}x_{22}+w_{13}x_{23}\hphantom{00000} & w_{11}x_{22}+w_{12}x_{23}+w_{13}x_{24} \newline +w_{21}x_{31}+w_{22}x_{32}+w_{23}x_{33}\hphantom{00000} & +w_{21}x_{32}+w_{22}x_{33}+w_{23}x_{34} \newline +w_{31}x_{41}+w_{32}x_{42}+w_{33}x_{43}, \hphantom{00000} & +w_{31}x_{42}+w_{32}x_{43}+w_{33}x_{44} \newline \end{bmatrix} $$

那么卷积矩阵是什么呢？用另一种方式来表示卷积操作：

将$3 \times 3$ 的卷积核的卷积运算表示成一个$4 \times 16$的矩阵，如下图所示。

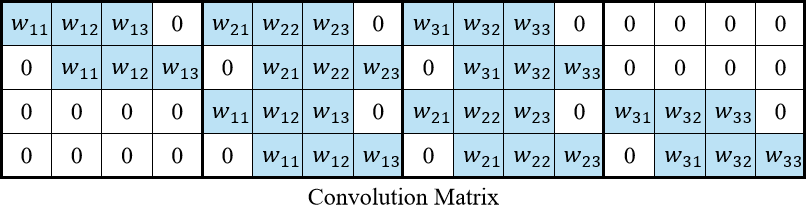
Source XuHao

每一行表示一次卷积操作。比如第一行：

Source XuHao

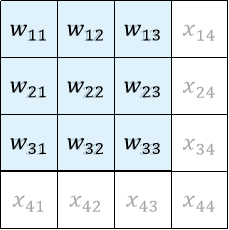
Source XuHao

就是由第一次卷积操作时卷积核在输入中的映射拉直而来的。可以看到，没有进行卷积计算的位置被补了零。

而后再将输入拉直成一个列向量，如下图所示，这样通过卷积矩阵$C$与输入向量$I$进行矩阵乘法，就能得到最后的输出$O$了。即$O=C I$

Source XuHao

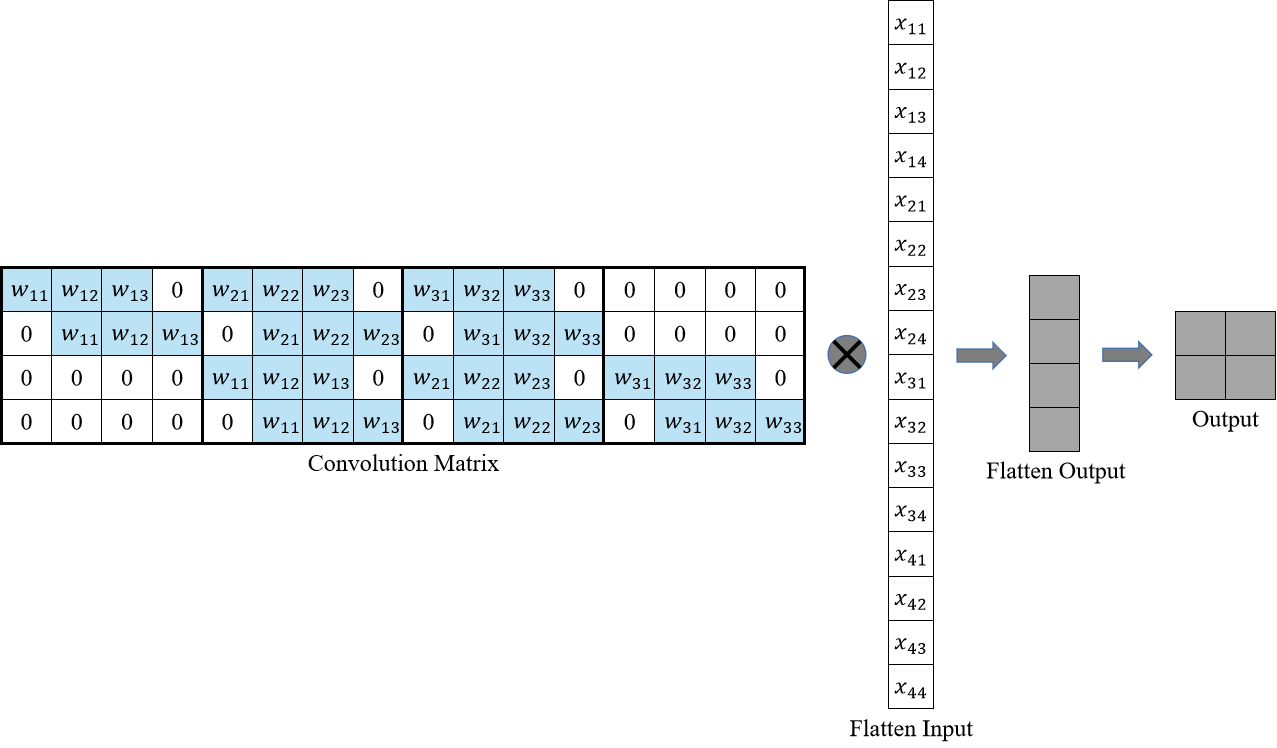
Source XuHao

卷积操作是将卷积矩阵与拉直的输入进行矩阵乘法，即$O=CI$，那么反卷积不就是卷积的反向操作，希望对卷积操作的输出进行反卷积操作，从而得到卷积操作的输入嘛。

那么我们可以有如下公式推导：

$$ O = CI \newline I = OC^T $$

所以我们只需要将卷积矩阵转置一下就可以得到转置卷积矩阵。

转置卷积矩阵

即如下图所示，转置卷积操作即可从转置卷积矩阵与拉直的输入进行举证乘法得到输出。

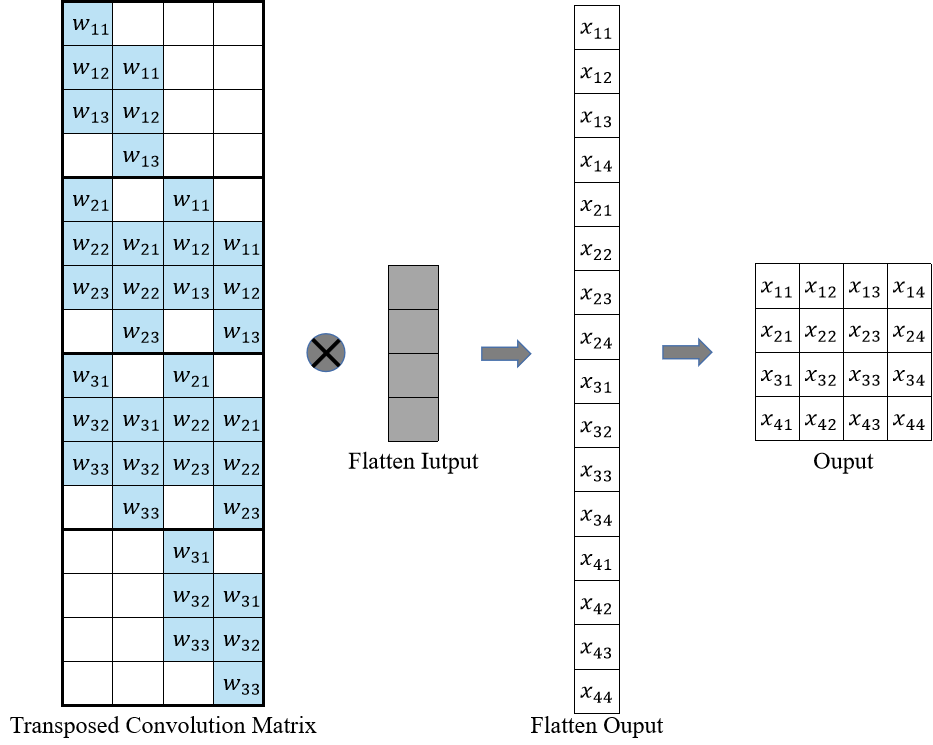
Source XuHao

注意：转置卷积矩阵中的权值不必要来自于原始的卷积矩阵，重要的是这些权值的布局时从卷积矩阵中来的。同时，转置卷积不保证恢复输入卷积操作的输入本身，而只是返回具有相同形状的特征图。

可以将卷积操作和转置卷积操作理解成一个卷积核使用卷积矩阵$C$进行正向操作或使用转置卷积矩阵$C^T$进行反向操作。

转置卷积的输出形状计算

我们可以通过卷积来模拟转置卷积。

如下左图，3×3 的卷积核在 4×4 的蓝色输入上进行没有 padding 和单位 stride 的卷积操作，得到 2×2 的灰色输出。

当反过来进行转置卷积操作的时候，想由 2×2 的蓝色输入，通过 3×3 的卷积核转置卷积得到 4×4的输出，那么就要对原输入产生 2×2 的padding。这里的卷积核大小和 stride 都是保持不变的。如下右图所示。

No padding, unit strides. Source Convolution arithmetic

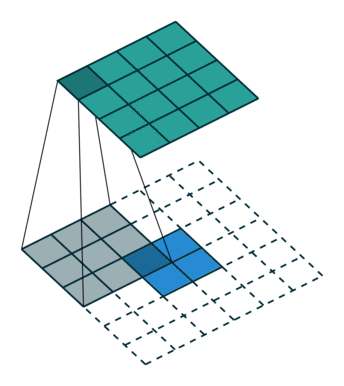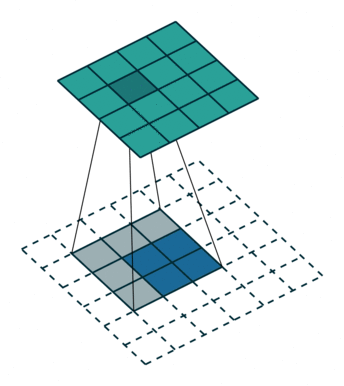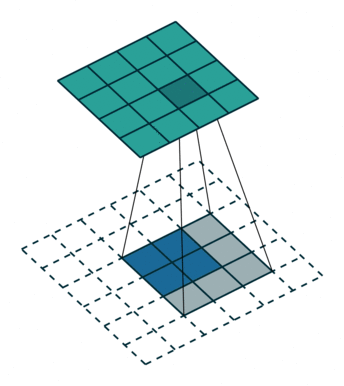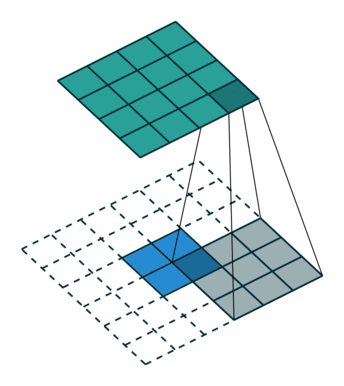
No padding, unit strides, transposed. Source Convolution arithmetic

那么到底该如何控制转置卷积输出的形状呢？下面会通过几个栗子，来粗略推导一下转置卷积输出形状的计算。

首先，$i, k, s, p, o$ 分别表示卷积操作的输入形状、卷积核大小、stride (步长) 大小、padding (填充) 大小、输出形状。

$i’, k’, s’, p’, o’$ 分表表示转置卷积操作的输入形状、卷积核大小、stride (步长) 大小、padding (填充) 大小、输出形状。

这里假设高宽的填充是相等的，不考虑不对称填充情况。

No zero padding, unit strides, transposed

这里的no zero padding指的是卷积操作的时候没有填充的。示意动画在上面给出。

这里 $i = 4, k = 3, s = 1, p = 0$ ，而 $i’ = 2, k’ = k = 3, s’ = s = 1, p’ = 2$ 。

这里的 $i’, k’, s’$ 都是固定的。为了能使转置卷积的输出与原卷积操作的输入保持一致，就需要做 $p’ = k -1$ 的填充。

则，当卷积操作是No zero padding, unit strides时，其对应的转置卷积有如下公式：

$$ i’ = o \newline k’=k \newline s’ = s \newline p’ = k - 1 $$

$$ o’ = i’+(k-1) $$

Zero padding, unit strides, transposed

前面是最简单的卷积操作没有填充的。那么我们卷积操作再加上padding会是什么样呢？

如下图，$i = 5, k = 4, s = 1, p = 2$ ，而 $i’ = 6, k’ = k = 4, s’ = s = 1, p’ = 1$

这里可以看到，为了让转置卷积的输出与卷积操作的输入形状相同，所以这里转置卷积时的padding 减小了。

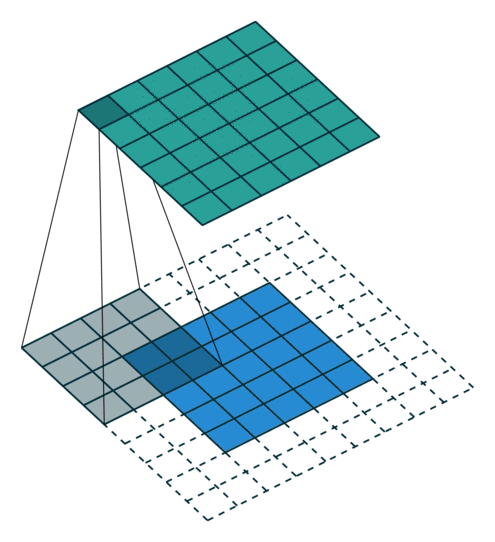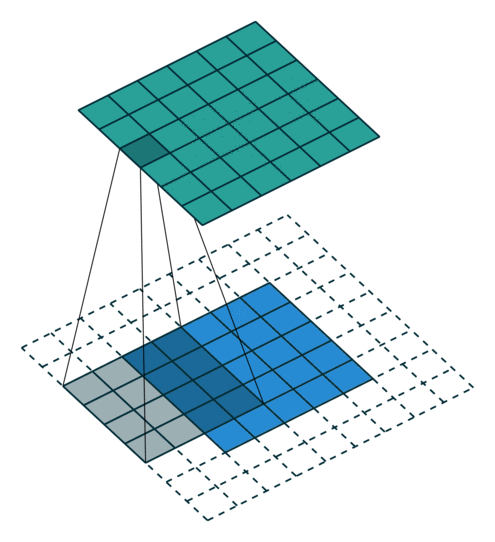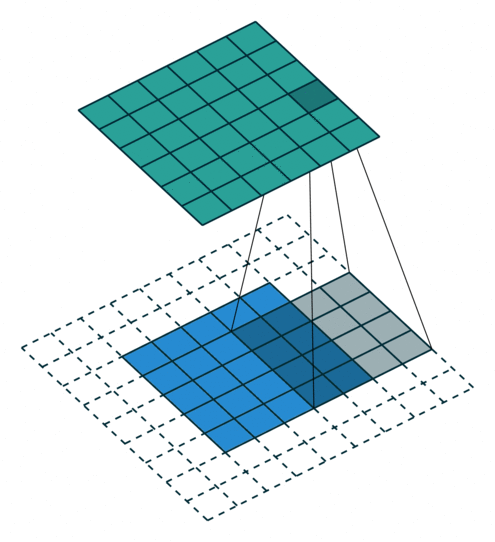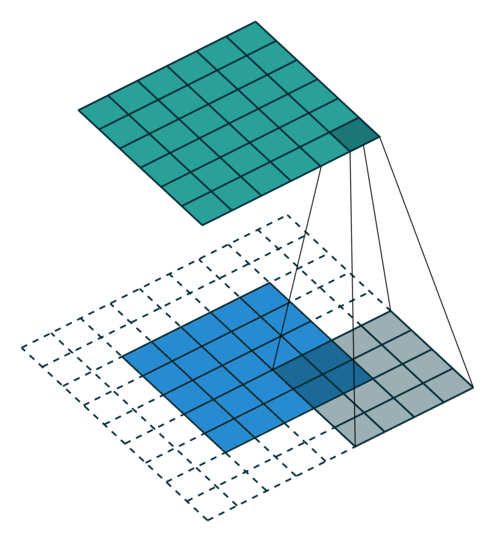
Padding, unit strides. Source Convolution arithmetic

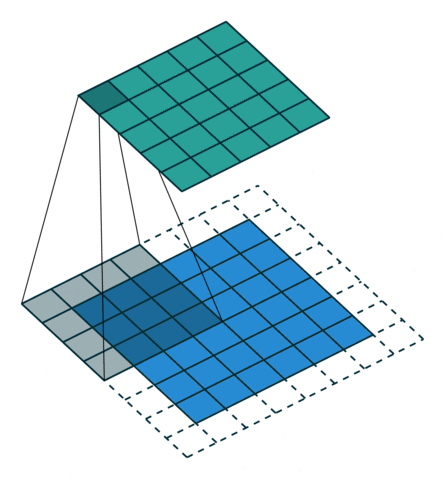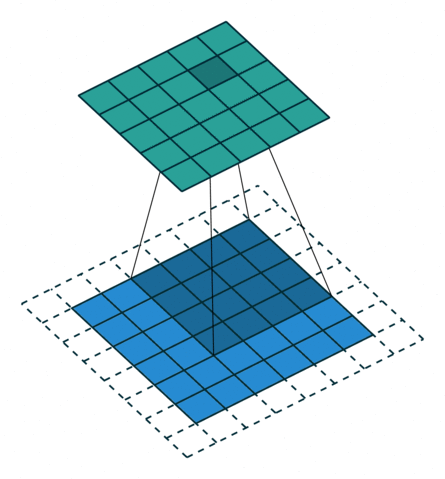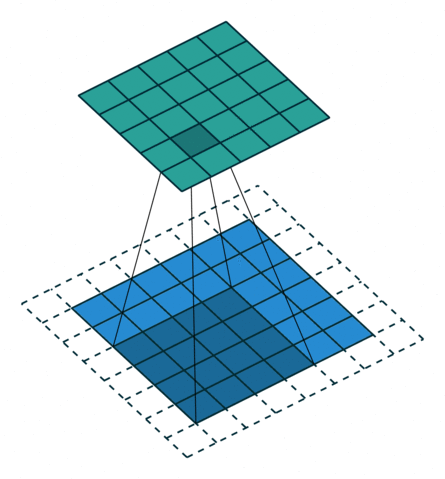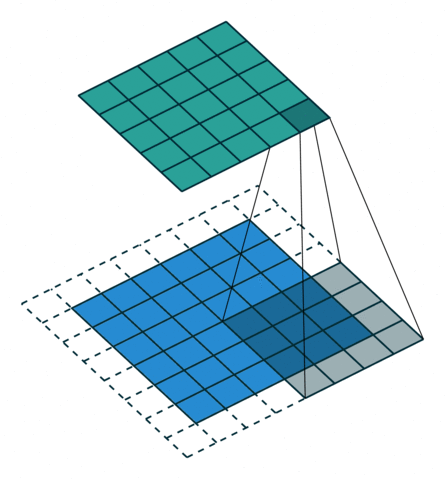
Padding, unit strides, transposed. Source Convolution arithmetic

则，有如下公式：

$$ i’ = o \newline k’=k \newline s’ = s \newline p’ = k - p - 1 \newline $$

$$ o’ = i’+(k-1)-2p $$

No zero padding, non-unit strides, transposed

前面的考虑了卷积操作时采用了padding。那么卷积操作没有padding，但不采用单位长度的stride又该怎么计算呢？

如下图，$i = 5, k = 3, s = 2, p = 0$ ，而 $i’ = 2, k’ = k = 3, s’ = 1, p’ = 2, \widetilde{i} = 1$ 。

这里 $\widetilde{i}$ 指的是在转置卷积单位输入之间补零的多少。在单位输入之间插入0是为了使卷积核移动的比单位步长更慢。这里 $\widetilde{i} = s - 1$ 。

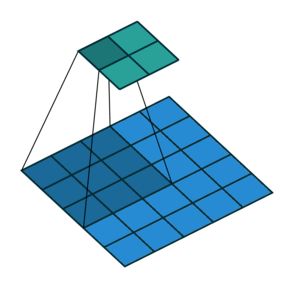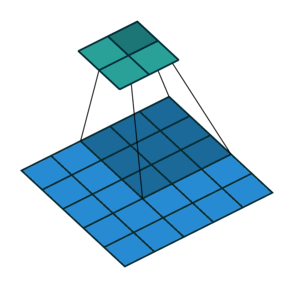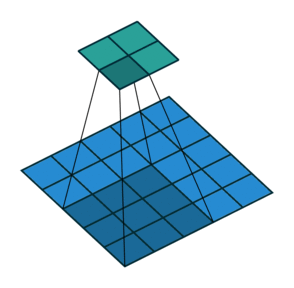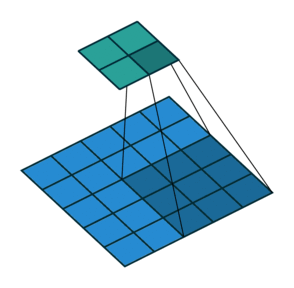
No padding, strides. Source Convolution arithmetic

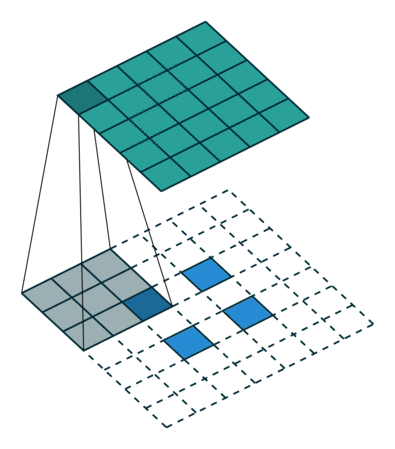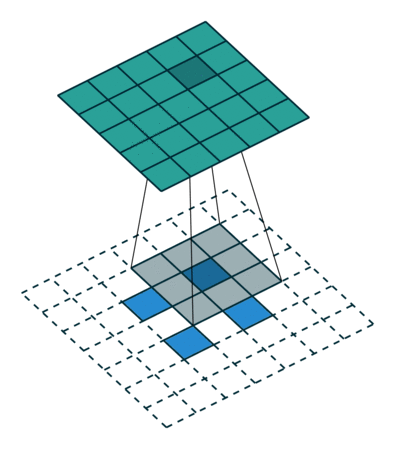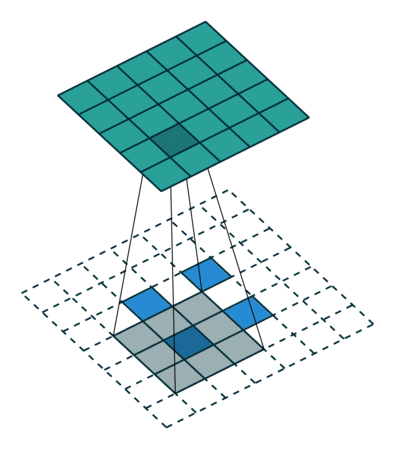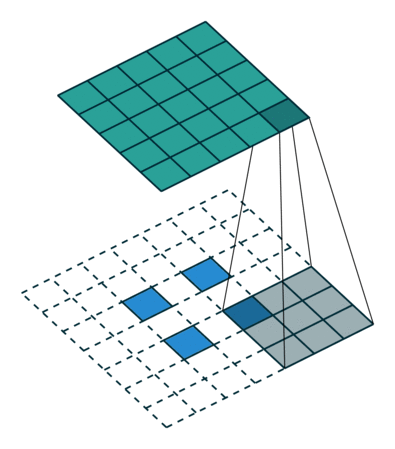
No padding, strides, transposed. Source Convolution arithmetic

假设，$p=0$，且输入 $i$ 满足 $i - k$ 是 $s$ 的倍数。则，有如下公式：

$$ i’ = o \newline k’= k \newline s’ = 1 \newline p’ = k - 1 \newline \widetilde{i} = s - 1 $$

$$ o’ = s(i’-1)+k $$

Zero padding, non-unit strides, transposed

最后再考虑最复杂的情况：卷积输入即使用了 padding，stride 也不是单位步长。

这样就能过得到一个对各种情况较为普适的公式。

如下图，$i = 5, k = 3, s = 2, p = 1$ ，而 $i’ = 3, k’ = k = 3, s’ = 1, p’ = 1, \widetilde{i} = 1$ 。

Padding, strides. Source Convolution arithmetic

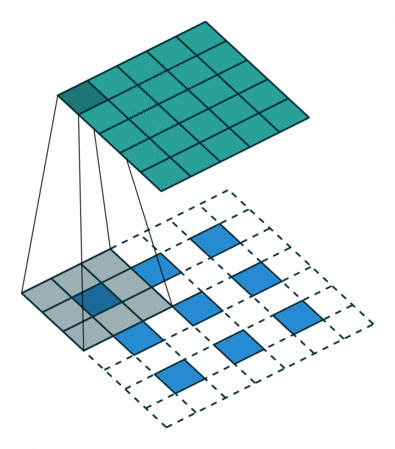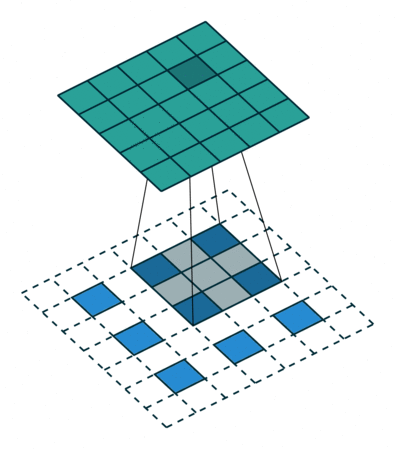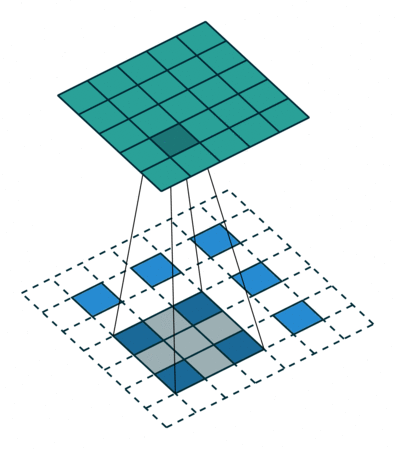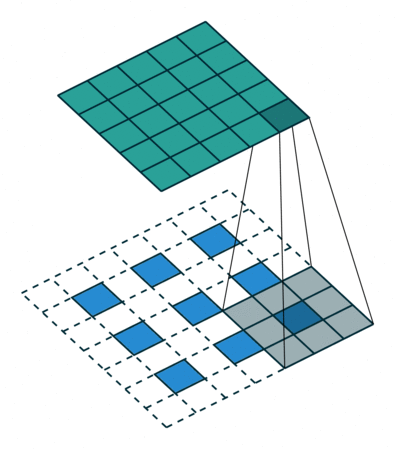
Padding, strides, transposed. Source Convolution arithmetic

结合前面的两种情况的公式，假设输入 $i$ 满足 $i + 2p - k$ 是 $s$ 的倍数，则有以下公式：

$$ i’ = o \newline k’= k \newline s’ = 1 \newline p’ = k - p - 1 \newline \widetilde{i} = s - 1 $$

$$ o’ = s(i’-1)+k-2p $$

有以上公式，基本可以应付转置卷积的大部分的计算。如有任何疑问，欢迎讨论，同时建议参考Dumoulin, Vincent, and Francesco Visin. “A guide to convolution arithmetic for deep learning.” arXiv preprint arXiv:1603.07285 (2016).

此外，转置卷积也有它的弊端：会产生棋盘效应。具体更详细的解释请参考：Odena, et al., “Deconvolution and Checkerboard Artifacts”, Distill, 2016. http://doi.org/10.23915/distill.00003

Reference

1. Jeremy Jordan. “An overview of semantic image segmentation.” https://www.jeremyjordan.me/semantic-segmentation/
2. Fei-Fei Li & Justin Johnson & Serena Yeung. “CS231n: Deep Learning for Computer Vision.” (2017). Lecture11. http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture11.pdf
3. Sultana, Farhana, Abu Sufian, and Paramartha Dutta. “Evolution of image segmentation using deep convolutional neural network: a survey.” Knowledge-Based Systems 201 (2020): 106062.
4. Kirillov, Alexander, et al. “Panoptic segmentation.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2019.
5. Long, Jonathan, Evan Shelhamer, and Trevor Darrell. “Fully convolutional networks for semantic segmentation.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2015.
6. Naoki, “Up-sampling with Transposed Convolution” https://naokishibuya.medium.com/up-sampling-with-transposed-convolution-9ae4f2df52d0
7. Dumoulin, Vincent, and Francesco Visin. “A guide to convolution arithmetic for deep learning.” arXiv preprint arXiv:1603.07285 (2016).
8. vdumoulin, fvisin. “Convolution arithmetic” https://github.com/vdumoulin/conv_arithmetic
9. Odena, et al., “Deconvolution and Checkerboard Artifacts”, Distill, 2016. http://doi.org/10.23915/distill.00003

× Hao Xu Blog

如果这篇文章对你有用,请随意打赏

2元 5元 10元 50元 100元 任意金额

2元

使用微信扫描二维码完成支付

• ← Previous Post
• Next Post →