209. Minimum Size Subarray Sum

Description

Given an array of positive integers nums and a positive integer target, return the minimal length of a subarray whose sum is greater than or equal to target. If there is no such subarray, return 0 instead.

Example 1:

Input: target = 7, nums = [2,3,1,2,4,3]
Output: 2
Explanation: The subarray [4,3] has the minimal length under the problem constraint.

Example 2:

Input: target = 4, nums = [1,4,4]
Output: 1

Example 3:

Input: target = 11, nums = [1,1,1,1,1,1,1,1]
Output: 0

Constraints:

1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 104

Follow up: If you have figured out the O(n) solution, try coding another solution of which the time complexity is O(n log(n)).

Brute Force

最直接的方法就是通过两重循环，枚举所有的子数组，然后计算子数组的和，如果大于等于target，就更新最小长度。
但是这种方法的时间复杂度是$O(n^2)$，不符合题目要求。

具体C++代码如下：

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        // int min_len = nums.size();
        int min_len = INT_MAX;
        for (int i = 0; i < nums.size(); i++) {
            int sum = 0;
            for (int j = i; j < nums.size(); j++) {
                sum += nums[j];
                if (sum >= target) {
                    min_len = min_len < j - i + 1 ? min_len : j - i + 1;
                    // min_len = std::min(min_len, j-i+1);
                    break;
                }
            }
            
        }
        return min_len == INT_MAX ? 0 : min_len;
    }
};

Two Pointers (Sliding Window)

通过双指针实现滑动窗口，可以将时间复杂度降低到$O(n)$。

【注意】：
该题目的数组元素都是正整数，滑动窗口的和是递增的，所以可以通过滑动窗口的和来判断窗口是否需要移动左指针。
外部for循环针对右指针right，内部while循环针对左指针left。
注意理解滑动窗口的思想和原理。其关键在于数组元素是正整数导致的窗口和的递增性。

你可能会想：for循环里面还有一个while循环，时间复杂度不是 $O(n^2)$ 吗？之所以还是 $O(n)$ ，是因为右指针right可以移动 n 次，左指针left也可以移动次。对于外循环的每次迭代，内循环不会运行 n 次。滑动窗口保证最多 2n 次窗口迭代。这就是所谓的摊销分析 (Amortized analysis) - 尽管for循环内迭代的最坏情况是$O(n)$，但当您考虑整个运行时时，它的平均值为$O(1)$算法。

具体C++代码如下：

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int min_len = INT_MAX;
        int left = 0;
        int sum = 0;
        for (int right = 0; right < nums.size(); right++) {
            sum += nums[right];
            while (sum >= target) {
                min_len = min_len < right - left + 1 ? min_len : right - left + 1;
                // min_len = std::min(min_len, right-left+1);
                sum -= nums[left++];
            }
        }
        return min_len == INT_MAX ? 0 : min_len;
    }
};

Binary Search

对于$O(n\ log\ n)$的解法，可以通过二分查找的方法实现。
大致思路是先计算前缀和，然后通过二分查找找到对于每个起点i，满足sum[j] - sum[i] >= target的最小j。
同样需要注意的是，该题目的数组元素都是正整数，前缀和是递增的，所以可以通过前缀和来判断二分查找的方向。

具体C++代码如下：

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int min_len = INT_MAX;
        vector<int> prefix_sum(nums.size() + 1, 0);

        for (int i = 1; i <= nums.size(); i++)    prefix_sum[i] = prefix_sum[i - 1] + nums[i - 1];

        for (int i = 0; i < nums.size(); i++) {
            int left = i + 1;
            int right = nums.size();
            int result = -1;
            while (left <= right) {
                int middle = left + ((right - left) >> 1);
                if (prefix_sum[middle] - prefix_sum[i] < target) {
                    left = middle + 1;
                } else {
                    right = middle - 1;
                    result = middle;
                }
            }
            if (result != -1)   min_len = min_len < result - i ? min_len : result - i;
        }
        return min_len == INT_MAX ? 0 : min_len;
    }
};

59. Spiral Matrix II

Description

Given a positive integer n, generate an n x n matrix filled with elements from 1 to $n^2$ in spiral order.

Example 1:

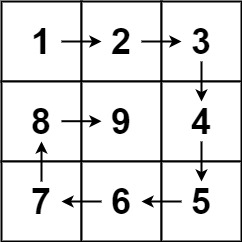
Input: n = 3
Output: [[1,2,3],[8,9,4],[7,6,5]]

Example 2:

Input: n = 1
Output: [[1]]

Constraints:

1 <= n <= 20

解题思路

这题主要是模拟螺旋矩阵的生成过程，需要注意的是边界条件的处理。核心思想是解码底层模式。这可以通过模拟模式并找到适用于任何给定 n 的通用表示来完成。

Traverse Layer by Layer in Spiral Form 螺旋式逐层遍历

Intuition

如果我们尝试为给定的 $n$ 构建一种模式，我们会观察到该模式在完成围绕矩阵的一次循环遍历后会重复。我们将这种循环遍历称为层。我们从外层开始遍历，并在每次迭代中向内层移动。

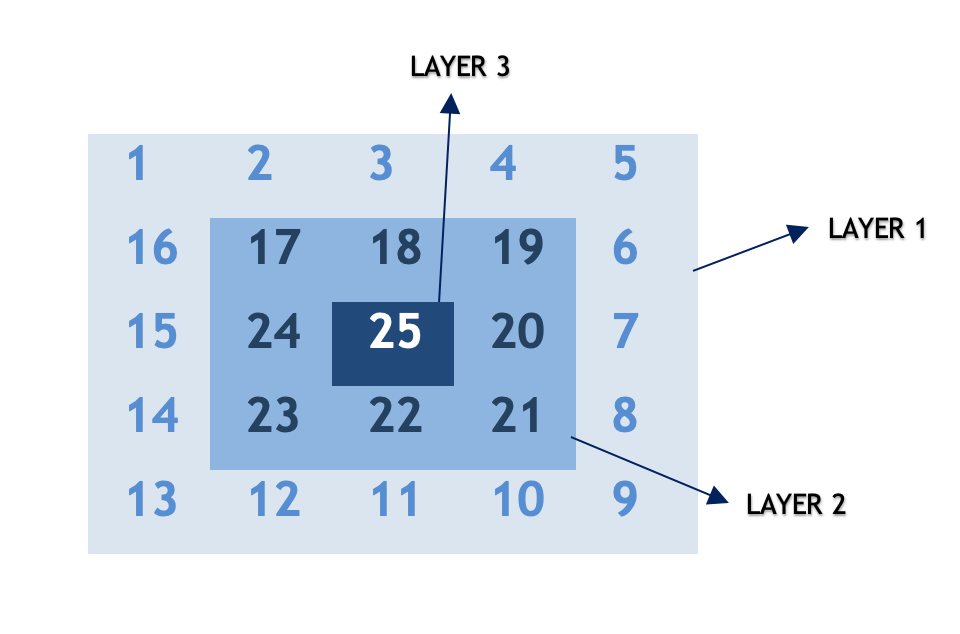
Spiral Layer

Algorithm 算法

Let’s devise an algorithm for the spiral traversal:
让我们设计一个螺旋遍历的算法：

We can observe that, for any given $n$, the total number of layers is given by :
我们可以观察到，对于任何给定的 $n$ ，总层数由下式给出：$$layers = \lceil \frac{n+1}{2} \rceil$$

This works for both even and odd $n$.
这适用于偶数和奇数 n 。

Example
例子

For $n=3, layers=2$
For $n=6$, total $layers=3$

Also, for each layer, we traverse in at most 4 directions :
此外，对于每一层，我们最多遍历 4 个方向：

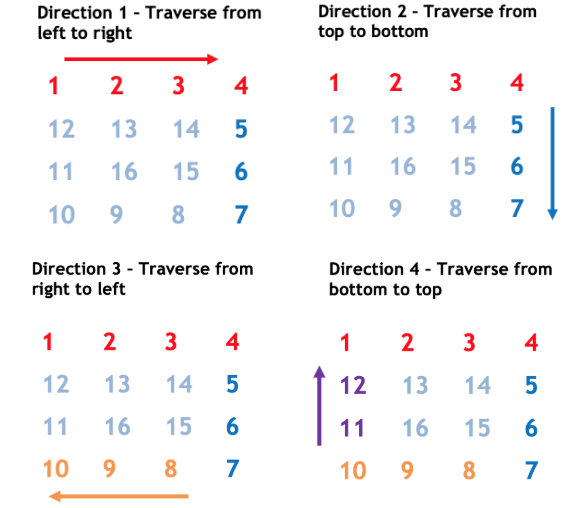
In every direction, either row or column remains constant and other parameter changes (increments/decrements).
在每个方向上，行或列保持不变，而其他参数发生变化（增量/减量）。

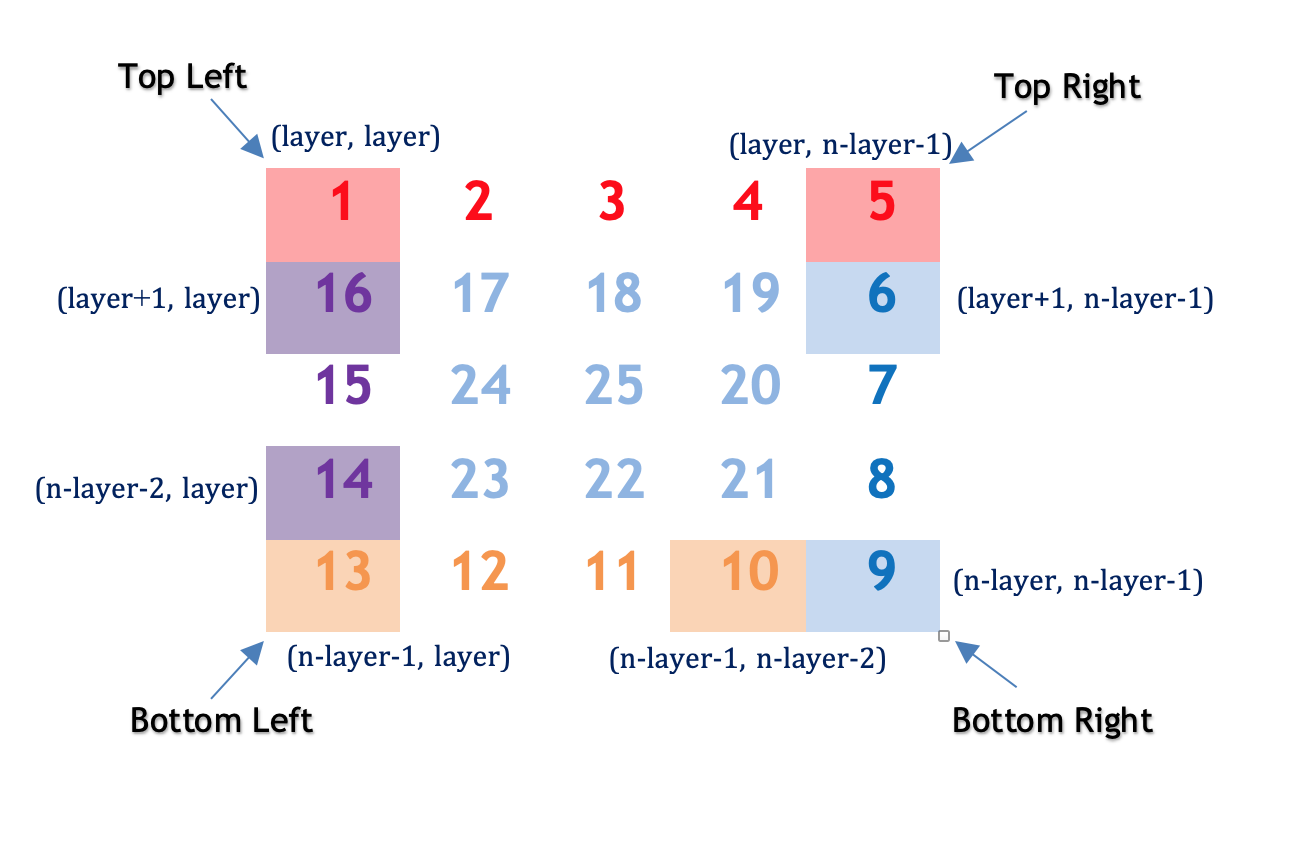
Direction 1: From top left corner to top right corner.
方向1：从左上角到右上角。
The row remains constant as $layer$ and column increments from $layer$ to $n−layer−1$
行保持不变为 $layer$ ，列从 $layer$ 递增到 $n−layer−1$

Direction 2: From top right corner to the bottom right corner.
方向2：从右上角到右下角。
The column remains constant as $n−layer−1$ and row increments from $layer+1$ to $n−layer$. 列保持不变为 $n−layer−1$ ，行从 $layer+1$ 到 $n−layer$ 。

Direction 3: From bottom right corner to bottom left corner.
方向3：从右下角到左下角。
The row remains constant as $n−layer−1$ and column decrements from $n−layer−2$ to $layer$. 行保持不变为 $n−layer−1$ ，列从 $n−layer−2$ 递减到 $layer$ 。

Direction 4: From bottom left corner to top left corner.
方向4：从左下角到左上角。
The column remains constant as $layer$ and column decrements from $n−layer−2$ to $layer+1$.
该列保持不变为 $layer$ ，并且列从 $n−layer−2$ 递减到 $layer+1$ 。

This process repeats $(n+1)/2$ times until all layers are traversed.
此过程重复 $(n+1)/2$ 次，直到遍历完所有层。

Spiral Details

Code

详细的C++代码如下：

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> matrix(n, vector<int>(n, 0));
        int num = 1;
        for (int layer = 0; layer < (n+1)/2; layer++){
            for (int ptr = layer; ptr < n-layer; ptr++) {
                matrix[layer][ptr] = num++;
            }
            for (int ptr = layer + 1; ptr < n-layer; ptr++) {
                matrix[ptr][n-layer-1] = num++;
            }
            for (int ptr = n-layer-2; ptr >= layer; ptr--) {
                matrix[n-layer-1][ptr] = num++;
            }
            for (int ptr = n-layer-2; ptr > layer; ptr--) {
                matrix[ptr][layer] = num++;
            }
        }
        return matrix;
    }
};

时间复杂度：$O(n^2)$

Kamacoder 58. Interval Sum

Description

58. 区间和（第九期模拟笔试）
给定一个整数数组 Array，请计算该数组在每个指定区间内元素的总和。

输入描述
第一行输入为整数数组 Array 的长度 n，接下来 n 行，每行一个整数，表示数组的元素。随后的输入为需要计算总和的区间下标：a，b （b > = a），直至文件结束。

输出描述
输出每个指定区间内元素的总和。

输入示例

输出示例

3
9

数据范围：

0 < n <= 100000

Solution

此题由于暴力解法的时间复杂度过高，所以可以考虑使用前缀和的方法进行优化。

#include <iostream>
#include <vector>

int main() {
    int num, interval_a, interval_b;
    std::cin >> num;

    // 初始化数组和前缀和数组
    std::vector<int> arr(num, 0);
    std::vector<int> prefix_sum(num + 1, 0);

    // 输入数组
    for (int i = 0; i < num; i++) {
        std::cin >> arr[i];
    }

    // 构造前缀和数组
    for (int i = 1; i <= num; i++) {
        prefix_sum[i] = prefix_sum[i - 1] + arr[i - 1];
    }

    // 处理查询
    while (std::cin >> interval_a >> interval_b) {
        if (interval_a >= 0 && interval_b < num) {
            std::cout << prefix_sum[interval_b + 1] - prefix_sum[interval_a] << std::endl;
        } else {
            std::cerr << "Invalid interval range." << std::endl;
        }
    }

    return 0;
}

上面是我自己写的代码，相较于下方标准答案，有一些细节问题，比如prefix_sum数组的大小，以及查询的范围。
不仅在计算前缀和的的时候增加了复杂度，并且在查询的时候需要进行判断，增加了代码的复杂度。

#include <iostream>
#include <vector>

int main() {
    int num, interval_a, interval_b;
    std::cin >> num;

    std::vector<int> arr(num, 0);
    std::vector<int> prefix_sum(num, 0);

    std::cin >> arr[0];
    prefix_sum[0] = arr[0];
    for (int i = 1; i < num; i++) {
        std::cin >> arr[i];
        prefix_sum[i] = prefix_sum[i - 1] + arr[i];
    }

    while (std::cin >> interval_a >> interval_b) {
        if (interval_a == 0) {
            std::cout << prefix_sum[interval_b] << std::endl;
        } else {
            std::cout << prefix_sum[interval_b] - prefix_sum[interval_a - 1] << std::endl;
        }
    }

    return 0;
}

Kamacoder 44. Developers Purchase Land

Description

44. 开发商购买土地（第五期模拟笔试）
题目描述
在一个城市区域内，被划分成了 $n \times m $ 个连续的区块，每个区块都拥有不同的权值，代表着其土地价值。目前，有两家开发公司，A 公司和 B 公司，希望购买这个城市区域的土地。

现在，需要将这个城市区域的所有区块分配给 A 公司和 B 公司。

然而，由于城市规划的限制，只允许将区域按横向或纵向划分成两个子区域，而且每个子区域都必须包含一个或多个区块。为了确保公平竞争，你需要找到一种分配方式，使得 A 公司和 B 公司各自的子区域内的土地总价值之差最小。

注意：区块不可再分。

输入描述
第一行输入两个正整数，代表 n 和 m。

接下来的 n 行，每行输出 m 个正整数。

输出描述
请输出一个整数，代表两个子区域内土地总价值之间的最小差距。

输入示例

输出示例

提示信息
如果将区域按照如下方式划分：

1 2 | 3
2 1 | 3
1 2 | 3

两个子区域内土地总价值之间的最小差距可以达到 0。

数据范围：

1 <= n, m <= 100；
n 和 m 不同时为 1。

Solution

可考虑使用前缀和的方法计算前 $i$ 行或前 $j$ 列的和。

下方代码需要注意的是由于代码网页需要手机号登录，并没有进行验证。

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int num_rows, num_cols, sum;
    cin >> num_rows >> num_cols;
    vector<vector<int>> matrix(num_rows, vector<int>(num_cols, 0));
    vector<int> sum_rows(num_rows, 0);
    vector<int> sum_cols(num_cols, 0);
    for (int row = 0; row < num_rows; row++) {
        for (int col = 0; col < num_cols; col++) {
            cin >> matrix[row][col];
            sum_rows[row] += matrix[row][col];
            sum_cols[col] += matrix[row][col];
            sum += matrix[row][col];
        }
    }
    
    // int left, right = 0;
    int res = INT_MAX;
    // int target = sum >> 1;
    // int middle = left + ((right - left) >> 1);
    
    // while (left <= right) {
        // if sum_rows[left] 
    // }

    for (int row = 0; row < num_rows; row++) {
        res = res < abs(sum - sum_rows[row] - sum_rows[row]);
    }
    
    for (int col = 0; col < num_cols; col++) {
        res = res < abs(sum - sum_cols[col] - sum_cols[col]);
    }
    
    cout << result << endl;
    
    return res;
}

Reference

代码随想录
 LeetCode 209. Minimum Size Subarray Sum
LeetCode 59. Spiral Matrix II
LeetCode 59. Spiral Matrix II Solution
一入循环深似海 | LeetCode：59.螺旋矩阵II
kamacoder 58. Interval Sum
kamacoder 44. Developers Purchase Land

「如果这篇文章对你有用,请随意打赏」

代码随想录Leetcode Day2 Array Part 2

209. Minimum Size Subarray Sum

Description

Brute Force

Two Pointers (Sliding Window)

Binary Search

59. Spiral Matrix II

Description

解题思路

Intuition

Algorithm 算法

Code

Kamacoder 58. Interval Sum

Description

Solution

Kamacoder 44. Developers Purchase Land

Description

Solution

Reference

CATALOG

FEATURED TAGS

FRIENDS