Hash Table

Introduction

哈希表 (Hash Table): 也叫做散列表。是根据关键码值 (Key Value) 直接进行访问的数据结构。

哈希表通过「键$key$」和「映射函数 $Hash(key)$」计算出对应的「索引 $index$」，把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做「哈希函数（散列函数）」，存放记录的数组叫做「哈希表（散列表）」。

哈希表的关键思想是使用哈希函数，将键映射到对应表的某个区块中。我们可以将算法思想分为两个部分:

向哈希表中插入一个关键码值:哈希函数决定该关键字的对应值应该存放到表中的哪个区块，并将对应值存放到该区块中。
在哈希表中搜索一个关键码值:使用相同的哈希函数从哈希表中查找对应的区块，并在特定的区块搜索该关键字对应的值。
哈希表的原理示例图如下所示: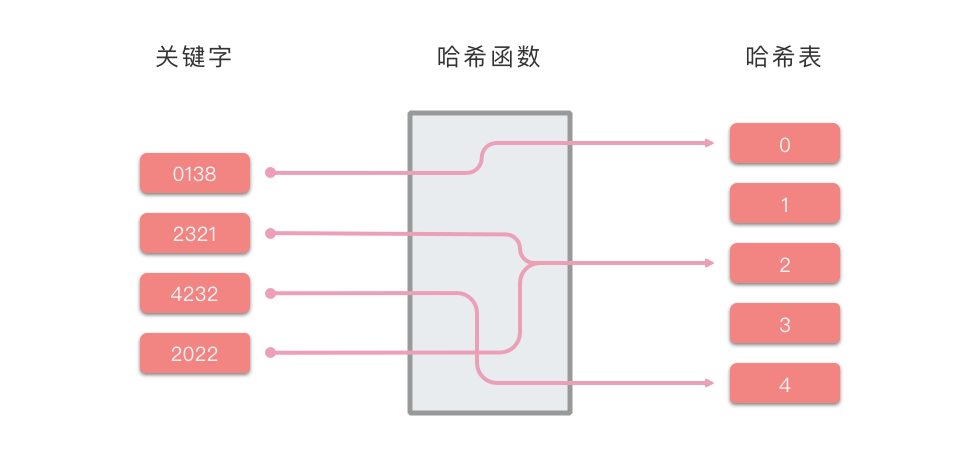

在上图例子中，我们使用 $index = Hash(key) = key // 1000$ 作为哈希函数。 $//$符号代表整除。我们以这个例子来说明一下哈希表的插入和查找策略。

向哈希表中插入一个关键码值: 通过哈希函数解析关键字，并将对应值存放到该区块中。
- 比如：$0138$通过哈希函数$ Hash(0138) = 0138 // 1000 $ ，得出应将 $0138$ 分配到$0$所在的区块中。
在哈希表中搜索一个关键码值: 通过哈希函数解析关键字，并在特定的区块搜索该关键字对应的值。
- 比如: 查找 $2321$，通过哈希函数，得出 $2321$ 应该在 $2$ 所对应的区块中。然后我们从 $2$ 对应的区块中继续搜索，并在 $2$ 对应的区块中成功找到了$2321$。
- 比如：查找 $3214$，通过哈希函数，得出 $3214$ 应该在 $3$ 所对应的区块中。然后我们从 $3$ 对应的区块中继续搜索，但并没有找到对应值，则说明 $3214$ 不在哈希表中。

哈希表在生活中的一个常见例子就是「查字典」。

比如为了查找 「赞」 这个字的具体意思，我们在字典中根据这个字的拼音索引 zan，查找到对应的页码为 $599$。然后我们就可以翻到字典的第 $599$ 页查看 「赞」 字相关的解释了。

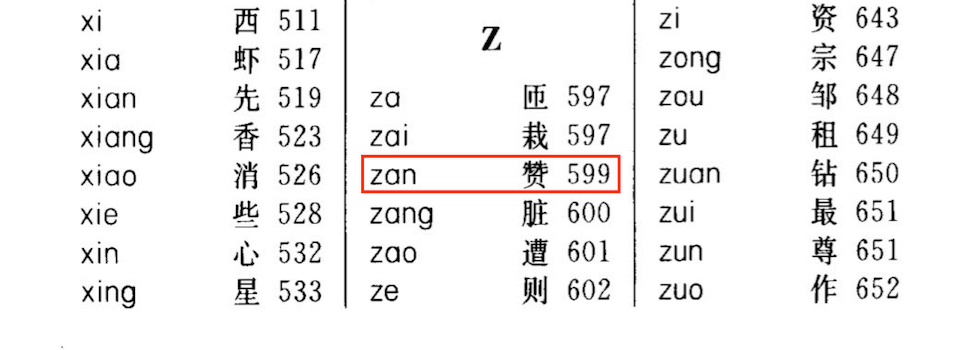
Dictionary

在这个例子中：

存放所有拼音和对应地址的表可以看做是 「哈希表」。
「赞」 字的拼音索引 zan 可以看做是哈希表中的 「关键字 $key$」。
根据拼音索引 zan 来确定字对应页码的过程可以看做是哈希表中的 「哈希函数 $Hash(key)$」。
查找到的对应页码 $599$ 可以看做是哈希表中的 「哈希地址 $value$」。

Hash Function

哈希函数 (Hash Function): 将哈希表中元素的关键键值映射为元素存储位置的函数。

哈希函数是哈希表中最重要的部分。一般来说，哈希函数会满足以下几个条件：

哈希函数应该易于计算，并且尽量使计算出来的索引值均匀分布。
哈希函数计算得到的哈希值是一个固定长度的输出值。
如果 $Hash(key1) \neq Hash(key2)$，那么 $key1$ 和 $key2$ 一定不相等。
如果 $Hash(key1) = Hash(key2)$，那么 $key1$ 和 $key2$可能相等，也可能不相等(会发生哈希碰撞)。

在哈希表的实际应用中，关键字的类型除了数字类，还有可能是字符串类型、浮点数类型、大整数类型，甚至还有可能是几种类型的组合。一般我们会将各种类型的关键字先转换为整数类型，再通过哈希函数，将其映射到哈希表中。

而关于整数类型的关键字，通常用到的哈希函数方法有：直接定址法、除留余数法、平方取中法、基数转换法、数字分析法、折叠法、随机数法、乘积法、点积法等。下面我们介绍几个常用的哈希函数方法。

直接定址法

直接定址法: 取关键字本身 / 关键字的某个线性函数值作为哈希地址。即: $Hash(key) = key$ 或者 $Hash(key) = a \times key + b$ ，其中 $a$ 和 $b$ 为常数。
这种方法计算最简单，且不会产生冲突。适合于关键字分布基本连续的情况，如果关键字分布不连续，空位较多，则会造成存储空间的浪费。

除留余数法

除留余数法: 假设哈希表的表长为 $m$，取一个不大于 $m$ 但接近或等于 $m$ 的质数，利用取模运算，将关键字转换为哈希地址。即: $Hash(key) = key \mod p$，其中 $p$ 为不大于 $m$ 的质数。
这也是一种简单且常用的哈希函数方法。其关键点在于 $p$ 的选择。根据经验而言，一般 $m$ 取素数或者 $m$，这样可以尽可能的减少冲突。

Hash Collision

哈希冲突 (Hash Collision)：不同的关键字通过同一个哈希函数可能得到同一哈希地址，即 $Hash(key1) = Hash(key2)$，但是 $key1 \neq key2$，这种现象称为哈希冲突。

理想状态下，我们的哈希函数是完美的一对一映射，即一个关键字 $(key)$ 对应一个索引 $(index)$，不需要处理冲突。但是一般情况下，不同的关键字 $(key)$ 通过哈希函数映射到同一个索引 $(index)$ 的情况是非常常见的。这种情况就是哈希冲突。

设计再好的哈希函数也无法完全避免哈希冲突。所以就需要通过一定的方法来解决哈希冲突问题。常用的哈希冲突解决方法主要是两类：「开放地址法 (Open Addressing)」 和 「链地址法 (Chaining)」。

开放地址法

开放地址法 (Open Addressing): 指的是将哈希表中的「空地址」向处理冲突开放。当哈希表未满时，处理冲突时需要尝试另外的单元，直到找到空的单元为止。

当发生冲突时，开放地址法按照下面的方法求得后继哈希地址: $$H(i) = (Hash(key) + F(i)) \mod m, i = 1, 2, 3, \ldots, n$$

$H(i)$ 是在处理冲突中得到的地址序列。即在第1次冲突 $(i=1)$ 时经过处理得到一个新地址 $H(1)$，如果在 $H(1)$ 处仍然发生冲突 $(i=2)$ 时经过处理时得到另一个新地址 $H(2)$ …… 如此下去，直到求得的 $H(n)$ 不再发生冲突。
$Hash(key)$ 是哈希函数，$m$ 是哈希表表长，对哈希表长取余的目的是为了使得到的下一个地址一定落在哈希表中。
$F(i)$ 是冲突解决方法，取法可以有以下几种:
- 线性探测法: $F(i) = 1,2,3, \ldots, m-1$ 。即依次探测下一个地址。
- 二次探测法: $F(z) = 1^2, -1^2, 2^2, -2^2, \ldots, \pm n^2 (n \leq m/2)。$ 即探测下一个地址的平方。
- 伪随机数序列: $F(i) = 伪随机数序列。$ 即通过伪随机数序列来探测下一个地址。

举个例子说说明一下如何用以上三种冲突解决方法处理冲突，并得到新地址 $H(i)$。例如，在长度为 $11$ 的哈希表中已经填有关键字分别为 $28、49、18$ 的记录 (哈希函数为 $Hash(key) = key \mod 11$)。现在将插入关键字为 $38$ 的新纪录。根据哈希函数得到的哈希地址为 $5$，产生冲突。接下来分别使用这三种冲突解决方法处理冲突。

使用线性探测法: 得到下一个地址 $H(1) = (5 + 1) \mod 11 = 6$，仍然冲突；继续求出 $H(2) =(5+2) \mod 11 = 7$，仍然冲突；继续求出 $H(3) =(5 + 3) \mod 11 = 8$， $8$ 对应的地址为空，处理冲突过程结束，记录填入哈希表中索引为 $8$ 的位置。
使用二次探测法: 得到下一个地址 $H(1) =(5 + 1 \times 1) \mod 11 = 6$，仍然冲突；继续求出 $H(2) = (5 - 1 \times 1) \mod 11 = 4$，$4$ 对应的地址为空，处理冲突过程结束，记录填入哈希表中索引为 $4$ 的位置。
使用伪随机数序列：假设伪随机数为 $9$，则得到下一个地址 $H(1) = (9 + 5) \mod 11 = 3$，$3$ 对应的地址为空，处理冲突过程结束，记录填入哈希表中索引为 $3$ 的位置。
使用这三种方法处理冲突的结果如下图所示:

链地址法

链地址法 (Chaining): 将具有相同哈希地址的元素(或记录)存储在同一个线性链表中。

链地址法是一种更加常用的哈希冲突解决方法。相比于开放地址法，链地址法更加简单。

我们假设哈希函数产生的哈希地址区间为 $[0, m-1]$，哈希表的表长为 $m$。则可以将哈希表定义为一个有 $m$ 个头节点组成的链表指针数组 $T$。

这样在插入关键字的时候，我们只需要通过哈希函数 $Hash(key)$ 计算出对应的哈希地址 $i$，然后将其以链表节点的形式插入到以 $T[i]$ 为头节点的单链表中。在链表中插入位置可以在表头或表尾，也可以在中间。如果每次插入位置为表头，则插入操作的时间复杂度为 $O(1)$。
而在在查询关键字的时候，我们只需要通过哈希函数 $Hash(key)$ 计算出对应的哈希地址 $i$，然后将对应位置上的链表整个扫描一遍，比较链表中每个链节点的键值与查询的键值是否一致。查询操作的时间复杂度跟链表的长度 $k$ 成正比，也就是 $O(k)$。对于哈希地址比较均匀的哈希函数来说，理论上讲，$k = n // m$，其中 $k$ 为关键字的个数，$m$ 为哈希表的表长。

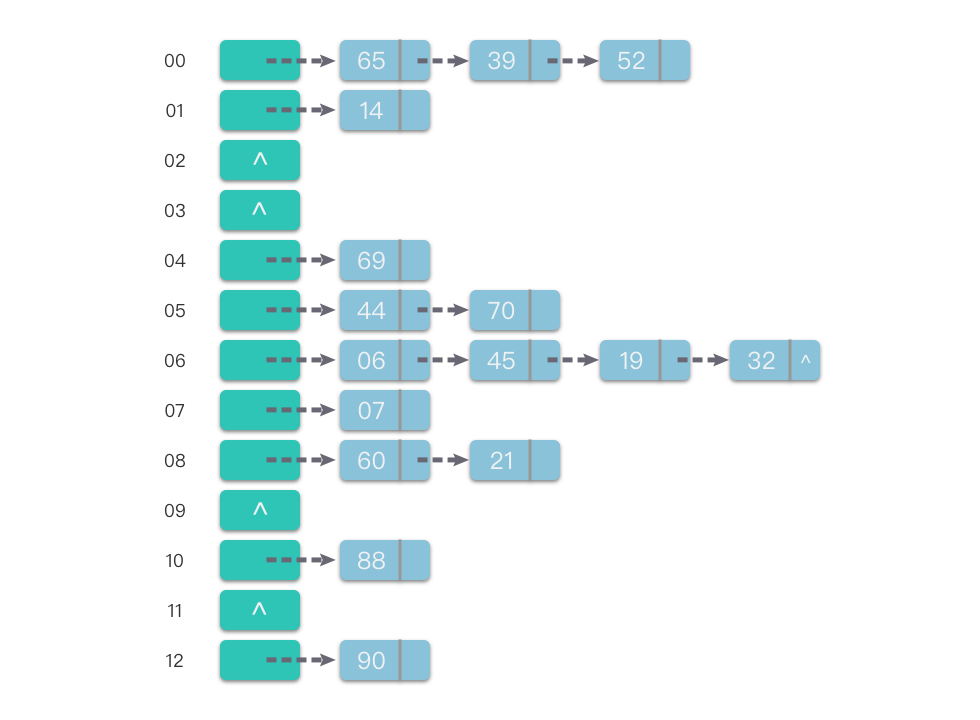
举个例子来说明如何使用链地址法处理冲突。假设现在要存入的关键字集合 $keys =［88, 60, 65, 69, 90, 39, 07, 06, 14, 44, 52, 70, 21, 45, 19, 32]$。再假定哈希函数为 $Hash(key) = key \mod 13$，哈希表的表长 $m = 13$，哈希地址范围为 $[0，m一1]$。将这些关键字使用链地址法处理冲突，并按顺序加入哈希表中(图示为插入链表表尾位置)，最终得到的哈希表如下图所示。 Chaining

上方所有内容都来自Datahale Leetcode 算法笔记 | 03.01.01 哈希表 (第 01 ~ 02 天)
搬运过来仅是为了方便自己复习，如有侵权请联系删除。

C++中的哈希表

C++中的哈希表主要是通过 array，set，map等容器实现的。array是一个固定大小的数组，set是一个集合，map是一个键值对。
其中，std::unordered_set 和 std::unordered_map，这两个容器是基于哈希表实现的，查询与增删效率都是 $O(1)$。在解决哈希表问题时应当优先考虑使用这两个容器。
std::set，std::multiset，std::map，std::multimap是基于红黑树实现的，查询与增删效率都是 $O(\log n)$。key值是有序的，但key不可以修改，改动key值会导致整棵树的错乱，所以只能删除和增加。两种 set 的区别是 std::multiset 允许重复元素。同理，std::multimap 允许重复的key。

Java中的哈希表主要是通过 HashMap 实现的，查询与增删效率都是 $O(1)$。
而TreeMap 是基于红黑树实现的，查询与增删效率都是 $O(\log n)$。

Python中的哈希表主要是通过 dict 实现的，查询与增删效率都是 $O(1)$。

242. Valid Anagram

Description

Given two strings s and t, return true if t is an anagram (An anagram is a word or phrase formed by rearranging the letters of a different word or phrase, using all the original letters exactly once.) of s, and false otherwise.

Example 1:

Input: s = "anagram", t = "nagaram"

Output: true

Example 2:

Input: s = "rat", t = "car"

Output: false

Constraints:

$1 <= s.length, t.length <= 5 \times 10^4$
s and t consist of lowercase English letters.

Follow up: What if the inputs contain Unicode characters? How would you adapt your solution to such a case?

Solution

对于 $O(n^2)$ 的暴力解法，这里不再赘述。

如果能够想到使用哈希表进行类似于词频统计来解决，那么这道题就会变得非常简单。

这里使用长度为 $26$ 的数组来模拟哈希表，数组的下标表示字母，数组的值表示字母出现的次数。当遍历字符串 $s$ 时，将对应字母的次数加一，遍历字符串 $t$ 时，将对应字母的次数减一。最后判断数组中的值是否全为 $0$ 即可。

class Solution {
public:
    bool isAnagram(string s, string t) {
        int freq[26] = {0};
        for (int i = 0; i < s.size(); i++) {
            freq[s[i]-'a']++;
        }
        for (int i = 0; i < t.size(); i++) {
            freq[t[i]-'a']--;
        }
        for (int i = 0; i < 26; i++) {
            if (freq[i] != 0) {
                return false;
            }
        }
        return true;
    }
};

时间复杂度为 $O(n)$，空间复杂度为 $O(1)$。

思考：如果两个字符串是异位词，那么他们长度一定相等。所以，可以先进行长度判断，如果相等再进行哈希表统计并且前两个循环可以进行合并。

349. Intersection of Two Arrays

Description

Given two integer arrays nums1 and nums2, return an array of their intersection (The intersection of two arrays is defined as the set of elements that are present in both arrays.). Each element in the result must be unique and you may return the result in any order.

Example 1:

Input: nums1 = [1,2,2,1], nums2 = [2,2]
Output: [2]

Example 2:

Input: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
Output: [9,4]
Explanation: [4,9] is also accepted.

Constraints:

1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 1000

Solution

此题可以同上题一样使用哈希表来统计两个数组中的元素，然后再进行比较。但是需要使用 set 来进行去重最后转换成 vector 输出。

下方提供两种解法，第一种使用 unsorted_set 直接统计 nums1 中的元素，然后再遍历 nums2，如果 nums2 中的元素在 set 中，则将其加入到 res 集合中。第二种和上题类似，使用一个长度为 $1001$ 的数组来统计 nums1 中的元素，然后再遍历 nums2，如果以 nums2 中的元素为下标的数组值不为 $0$，则将其加入到 res 集合中。
两者的时间复杂度都是 $O(n)$，空间复杂度都是 $O(n)$。但是在数据量较大的 case 中，第二种方法的效率会更高。

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> nums1_set(nums1.begin(), nums1.end());
        unordered_set<int> intersection;
        for (int num : nums2) {
            if (nums1_set.find(num) != nums1_set.end())      intersection.insert(num);
        }
        return vector<int>(intersection.begin(), intersection.end());
    }
};

这里需要注意 unordered_set<int> nums1_set(nums1.begin(), nums1.end()); 和 vector<int>(intersection.begin(), intersection.end()); 这两句代码可以实现集合和数组之间的转换。
此外，unsorted 的查找用法 nums1_set.find(num) != nums1_set.end()，如果 num 在 nums1_set 中，则 find 函数返回的迭代器不等于 end，否则等于 end。

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        int occur[1001] = {0};
        unordered_set<int> intersection;
        for (int num : nums1)     occur[num] = 1;
        for (int num : nums2) {
            if (occur[num] == 1)      intersection.insert(num);
        }
        return vector<int>(intersection.begin(), intersection.end());
    }
};

202. Happy Number

Description

Write an algorithm to determine if a number n is happy.

A happy number is a number defined by the following process:

Starting with any positive integer, replace the number by the sum of the squares of its digits.
Repeat the process until the number equals 1 (where it will stay), or it loops endlessly in a cycle which does not include 1.
Those numbers for which this process ends in 1 are happy. Return true if n is a happy number, and false if not.

Example 1:


Input: n = 19
Output: true

Explanation:
$1^2 + 9^2 = 82$
$8^2 + 2^2 = 68$
$6^2 + 8^2 = 100$
$1^2 + 0^2 + 0^2 = 1$

Example 2:


Input: n = 2
Output: false

Constraints:

$1 <= n <= 2^{31} - 1$

Solution

这题需要判断终止条件：当数字为 $1$ 时，返回 true；当数字重复出现时，返回 false。

这题的关键是判断数字是否重复出现。可以使用 set 来存储每次计算的结果，如果结果重复出现，则返回 false。

此外还需要注意如何计算每一位数字的平方和。这里可以使用 % 和 / 运算来分别得到数字的最后一位和去掉最后一位的数字。

class Solution {
public:
    bool isHappy(int n) {
        unordered_set<int> sum_set;
        while (sum_set.find(n) == sum_set.end()) {
            sum_set.insert(n);
            int sum = 0;
            while (n) {
                sum += (n%10) * (n%10);
                n /= 10;
            }
            if (sum == 1)   return true;
            else    n = sum;
        }
        return false;
    }
};

该解法的复杂度为 $O(log n)$，空间复杂度为 $O(log n)$。

1. Two Sum

Description

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.

You may assume that each input would have exactly one solution, and you may not use the same element twice.

You can return the answer in any order.

Example 1:


Input: nums = [2,7,11,15], target = 9
Output: [0,1]
Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].

Example 2:


Input: nums = [3,2,4], target = 6
Output: [1,2]

Example 3:


Input: nums = [3,3], target = 6
Output: [0,1]

Constraints:

$2 <= nums.length <= 10^4$
$-10^9 <= nums[i] <= 10^9$
$-10^9 <= target <= 10^9$
Only one valid answer exists.

Follow-up: Can you come up with an algorithm that is less than $O(n^2)$ time complexity?

Solution

此题有多种解法，这里主要使用哈希表来实现 $O(n)$ 的时间复杂度。

这里需要使用 unordered_map 来存储每个数字对应的下标。遍历数组时，如果 target - nums[i] 在 map 中，则返回对应下标，否则就将数字与下标的 pair 存入 map 中。

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> num_map;
        for (int i = 0; i < nums.size(); i++) {
            auto iter = num_map.find(target - nums[i]);
            if (iter == num_map.end())    num_map.insert(pair<int, int>(nums[i], i));
            else    return {i, iter->second};
        }
        return {};
    }
};

这题主要需要注意 C++ 中 map 和 unordered_map 的使用方法（如何创建，搜索，插入），以及如何返回 vector。

Reference

代码随想录
 Datawhale Leetcode 算法笔记 | 03.01.01 哈希表 (第 01 ~ 02 天)
242. Valid Anagram
349. Intersection of Two Arrays
202. Happy Number
1. Two Sum
C++ 容器类 <unordered_set>
C++ 容器类 <unordered_map>

「如果这篇文章对你有用,请随意打赏」

代码随想录Leetcode Day5 Hash Table Part 1

Hash Table

Introduction

Hash Function

直接定址法

除留余数法

Hash Collision

开放地址法

链地址法

C++中的哈希表

242. Valid Anagram

Description

Solution

349. Intersection of Two Arrays

Description

Solution

202. Happy Number

Description

Solution

1. Two Sum

Description

Solution

Reference

CATALOG

FEATURED TAGS

FRIENDS